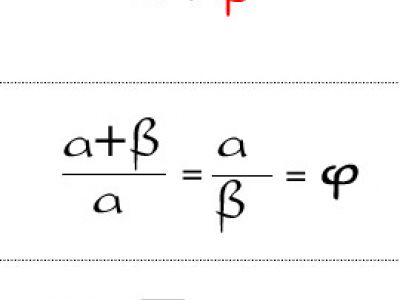"Güzellik bakanın gözündedir" klişesi büyük ölçüde doğrudur. Bir erkek bir Ferrari otomobilini olağanüstü güzel bulabilirken, bir kadın onu çok çirkin bulabilir. Bir kadın belirli bir elbiseyi çok güzel bulabilirken, bir erkek bu elbise hakkında olumsuz duygular besleyebilir. Öte yandan, yüzün güzel ve çekici algısı söz konusu olduğunda, yüzün şekli veya biçiminden kaynaklanan evrensel bir algı var gibi görünmektedir. Güzel ve çekici yüz kavramı kültür ve zamana göre değişebilmekle birlikte, evrensel olarak belli normlar taşıdığı düşünülmektedir. Bu evrensel çekicilik algısının biyolojik bir temeli var gibi görünmektedir. Güzellik diye adlandırılan kavram nasıl ortaya çıktı? Bunun matematiksel bir ifadesi var mı? İnsanoğlu yıllarca bu sorulara yanıt bulmaya çalışmıştır. Altın oran bu çabanın ürünüdür. Ancak büyük sorun, üç boyutlu yüzün sınırlı alanlarının 1:1.618 oranına sahip tek boyutlu bir oran sistemi ile doğrusal bir şekilde tanımlanabilmesidir. Marquardt maskeleri gibi altın oranı kullanan sistemler, yüzün herhangi bir bölümünü veya tüm yüzü iki boyutlu bir konfigürasyonda altın oranları kullanarak tanımlamaktadır.

Mısırlılar tarafından bilinen ve kullanılan, Eski Yunan'da ideal ifadesini bulan bu oran şöyle tanımlanabilir: Bir doğru parçası bir noktadan ikiye bölündüğünde; büyük parça = a, küçük parça = b ve a'nın b'ye oranı matematiksel olarak 1.61803 olduğunda buna "Phi, altın oran" denilmektedir. Bu değeri göstermek için İÖ 5. yüzyılda yaşamış heykeltraş Yunanlı Phidias’ın adının ilk harfi olan Ø = Phi kullanılmaktadır. Matematiksel olarak da ilginç bir sayıdır. Kendisinden 1 çıkarıldığında kendi tersi değerine ulaşmaktadır. 1 eklendiğinde kare değerine ulaşmaktadır. Bu özellikleriyle sayılar içerisinde tektir. Güzel ve dengeli olarak tanımladığımız her şeyde bu oranı görebiliriz.

1201 yılında matematikçi ve İtalya'nın Pisa'lı Leonardo Fibonacci bir sayı dizisi geliştirdi. Bu sayı, tavşanların çoğalması örneklendirilerek yapılmıştır ve eşsiz bir sayıdır. Dizideki her bir rakam, kendisinden önceki rakamların toplamından oluşmuştur: 0, 1, 1, 2, 3, 5, 8, 13… Dizideki her bir rakam gizemli sayı Pi ile ilişkilidir.

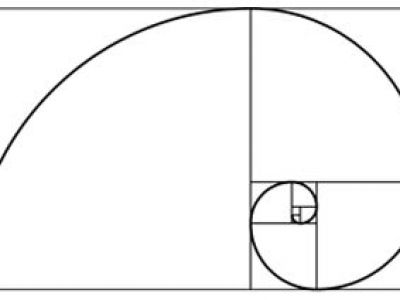
Altın oran, insanın doğada fark ettiği bir orandır. Uzun kenarı 1.61803, kısa kenarı 1 olan dikdörtgene altın dikdörtgen denilmektedir. Bu, göze en hoş görünen dikdörtgendir. Eski mimari yapılar bu dikdörtgenle yapılmıştır. İkiz kenar üçgende taban 1, ikiz kenarlar 1.61803 olursa buna altın üçgen denir. Bu altın üçgende taban açıların açıortayları, karşılarındaki kenarları altın oranda bölmektedir ve yeni altın üçgenler yapmaktadır. Bu yeni altın üçgenlerde baştaki açıortaylar tekrar çizildiğinde yeni altın üçgenler elde edilir. Bu çoğaltmayı altın dikdörtgen içinde yapabiliriz. Böylece logaritmik bir spiral elde edilir. Altın orana sahip örnekleri doğada görmekteyiz: Nautilus gibi bazı deniz kabukluları, ayçiçeği tohumlarının diziliminde vb. Hatta insanda doğum sonrası büyüme döneminde alt çenenin büyümesi bu logaritmik spiral ile olmaktadır.

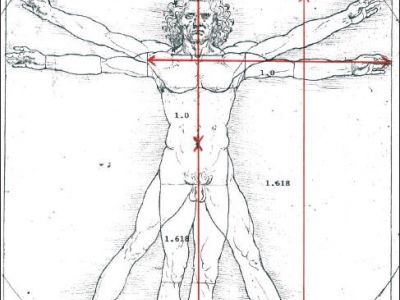
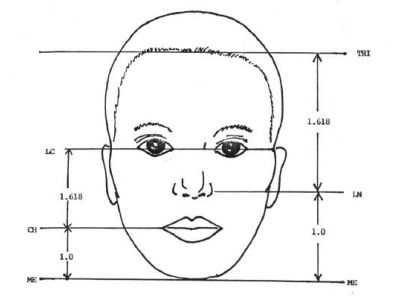
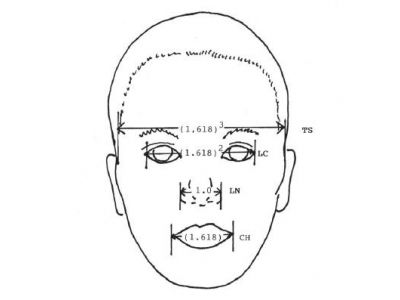
İnsan yüzündeki ve vücudundaki altın oranlar eski dönemlerden beri incelenmektedir. Leonardo da Vinci vücut ve yüz profilindeki altın oranı kullanmıştır. Örneğin, güzel olarak tanılanan bir yüzde burnun genişliğinin ağız genişliğine oranı 1:1.618'dir. İdeal bir insan vücudunda, ayağın altından göbeğe kadar olan mesafe, göbekten başın tepesine kadar olan mesafenin 1.618 katıdır. Göbek deliğinden tiroid kıkırdağına, adem elmasına kadar olan mesafe, tiroid kıkırdağından başın tepesine kadar olan mesafenin 1.618 katıdır. 

Altın orana dayanarak günümüzde yüz estetik analiz teknikleri kullanılmaktadır.;

• Bulardan ilki Baundun önerdiği "sirküler sektör analizidir". Bu analizde saç ön çizgisi trichion ve kulakta tragusu birleştiren hat yarıçap ve tragus merkezi olacak şekilde yüzün önünde yarım çember çizilmektedir. Bu çember burun ucu ve çeneden geçmelidir. Ayrıca kulakta tragus; trichion, nasion ve menton ile birleştirildiğinde aralarındaki açılar oluşmakta ve bunlar birbirlerine oranlandığında altın oranı vermektedir.

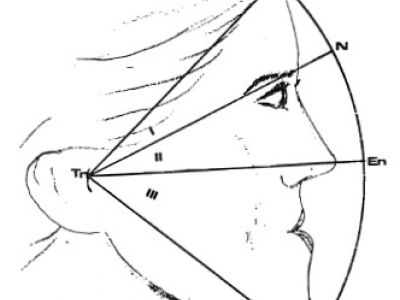
• Bir diğer yöntem Ricketts tarafından geliştirilmiştir. Bu yöntemde başın doğal pozisyonunda kulak tragusundan yatay bir hat çizilir. Buna paralel trichion, gözün dış köşesi kantusu, burun ucu, dudak birleşme noktası ve çenede mentondan paralel doğrular çizilmektedir. Bunlara burun ucu ile tragustan geçen dikmeler çizilir. Böylece yüz yan profilinde 3 adet altın dikdörtgen elde edilmektedir. Bu çizim üzerinden E-Me/Tri-Me= Phi, Tri-En/En-Me= Phi, En-Me/E-En = 2 Phi, Em-E/Me-Em = Phi, En-E/En-Em=Phi, Me-Em/En-Em= Phi vermektedir.

Atın oranı incelemek için "altın pergel" adı verilen bir alet geliştirilmiştir. Bu pergelin kolları her zaman altın oranı koruyacak şekilde açılır.

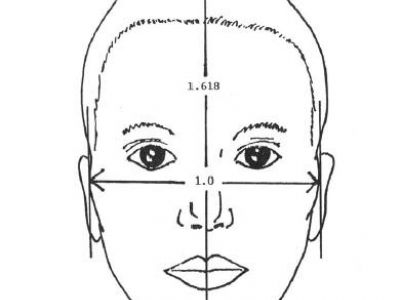
Yüzde çeşitli oranlar bulunsa da tam olarak güzellik kavramını ortaya koyan matematiksel formüller mevcut değildir. Öte yandan yüz öğeleri arasında belirlenen altın oran değerleri (1.61803…) sadece ideal insan yüzü için geçerlidir. Her ne kadar güzelliğin altın kuralı kendine güvenmek ve kendinin tek olduğunu anlamak olsa da son zamanlarda yüz güzelliği kararının otomatik verilebilmesi için çeşitli çalışmalar da yapılmaktadır. Kusursuz orantılara sahip bir insanın boyunun, başının yedi buçuk katı olduğu bilinmektedir. İnsan başına önden bakıldığında baş, yüksekliği 3.5 ve genişliği 2.5 oranlarında olan bir dikdörtgen meydana getirir. Gözler başın yüksekliğinin tam ortasında yer almaktadır. İki göz arasındaki mesafe bir gözün genişliği kadardır ve burun genişliğini belirler. Enine baş ölçüleri dört göz kadardır.

Antropometrik çalışmalarda insan yüzünde olduğu gibi güzel vücut ölçülerinde de oranlar aranmaktadır. 90 – 60 – 90 olarak kabul edilen ideal kadın ölçüleri aslında boy dikkate alınmadığında geçerlilik kazanmamaktadır. Venus de Milo’nun ölçüleri dikkate alınarak modelleme katsayısı ile yapılan değerlendirmelerde gerçek “altın oran” aşağıdaki şekilde ölçülmektedir. Gerçek “altın oran” = (98 – 70 – 100) × M, burada M = boy (cm) / 166. Formüle göre örneğin 150 cm boy için gerçek “altın oran” yaklaşık 88 – 63 – 90 olduğu halde 180 cm için 106 – 76 – 108 olmaktadır.